PiBrush — Painting with the Pi and XLoBorg

   

Turning an accelerometer into a paint brush with Raspberry Pi

Fred Sonnenwald, September 2013

[Featured in The MagPi, December 2013]

1. Introduction

Two weeks ago we participated in the Ideas Bazaar promoting Open Culture Tech, which I've translated to myself as a promoting how we can take finer control of technology for ourselves using low-cost and open technologies. "The proof is in the pudding" though, and actually demonstrating the point is a much more powerful argument. To this end we prepared our exhibit to show off various gizmos and widgets, including those based around Raspberry Pis. My contribution has been the PiBrush.

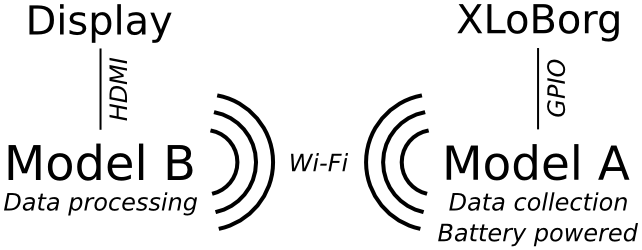
The PiBrush is an interactive art and technology exhibit (a very grand name for something so small) that simulates flicking paint off the end of a paintbrush onto canvas — as Jackson Pollock famously did in the 1940s and 50s. It utilizes two Raspberry Pis (one Model B and one Model A), a PiBorg XLoBorg accelerometer, a battery pack, a display, and two Wi-Fi dongles. The Model A is held by the user and waved around. It collects acceleration data with the XLoBorg, which it then transmits via Wi-Fi to the Model B, which processes the data collected into paint droplets and displays them on the screen, connected via HDMI.

Since the Bazaar, we've also added a physical reset button to save the current canvas and reset it to blank.

2. Programming

The hardware for this project is fairly straight forward. The XLoBorg plugs directly into the GPIO pins as a block, and a GPIO button is just a button connected between the ground and a GPIO pin — we've used BCM pin 17 or board pin 11. The software is where the challenge lies.

I developed the code from scratch, and doing so required a variety of knowledge. While I'd rate it as intermediate to advanced code to write, I'm hoping to shed enough light on it here that it is only beginner to intermediate to understand. The only real requirements are some basic familiarity with the Python programming language, networking (IP addresses), and basic Physics.

First, what code. The code is available on GitHub. This will always be the latest version. There's the python file accel_client.py which runs on the Model A and there's accel_server.py which runs on the Model B. The former reads in off the sensor and sends it across the network, the latter recieves the data, does processing, and displays the output on the screen.

2.1. accel_client.py

The client script is fairly straight forward. There are two unique points to consider though. Reading in the accelerometer data and the networking code. First though, we import the necessary libraries.

import socket
import XLoBorg
import time
import os

# network stufff
server = os.getenv('SERVER', 'modelb')
port = 5005

The XLoBorg has its own specific initialization function to be run at the start of a program using it. This uses the library to start communicating with the accelerometer over the I2C bus.

# setup for the accelerometer
XLoBorg.printFunction = XLoBorg.NoPrint
XLoBorg.Init()

# make the socket connection
sock = socket.socket(socket.AF_INET, socket.SOCK_DGRAM)

while True:
    message = '%+01.4f,%+01.4f,%+01.4f' \
            % XLoBorg.ReadAccelerometer()
    sock.sendto(message, (server, port))
    time.sleep(0.005)

2.2. accel_server.py

The server script is where the real meat of the programming is as it handles the simulation and display. Similar to accel_client.py, necessary libraries are first imported.

import socket
import select
import pygame
import time
import numpy
import math
import datetime
import random
import os
import RPi.GPIO as GPIO

math contains the functions like sin and cos which we use to handle some of the translation from where the accelerometer is to where the paint is on the screen. datetime is a bit of code that got accidentally left in from an old version — oops! (It was used to print the current date on the screen during debugging to tell if the program was frozen or not.) random is used to generate, as it sounds, random numbers. Finally RPi.GPIO is used to talk with the GPIO pins.

2.2.1. Initialization

# ==============
# initialization
# ==============

# port to listen on
port = 5005

# setup networking
sock = socket.socket(socket.AF_INET,
        socket.SOCK_DGRAM) # UDP
sock.bind(("0.0.0.0", port))
sock.setblocking(0)

# directory for saves
SAVEDIR = os.getenv('SAVEDIR', '.')

# setup GPIO input for reset
GPIO.setmode(GPIO.BCM)
GPIO.setup(17, GPIO.IN, pull_up_down=GPIO.PUD_UP)

# variable to store button state
button = 0

# screen solution
XRES = int(os.getenv('XRES', 1920))
YRES = int(os.getenv('YRES', 1080))

# setup display
pygame.init()
screen = pygame.display.set_mode((XRES, YRES))
# reset to white
screen.fill((255, 255, 255))
# push white
pygame.display.flip()

# length of moving average array
AL = 20

# accelerometer storage for moving average
AXa = numpy.zeros((AL, 1))
AYa = numpy.zeros((AL, 1))
AZa = numpy.ones((AL, 1))

# array index for accelerometer data
Ai = 0

An MA is the average of, in this case, the last 20 readings. Some sort of filtering is almost always necessary when dealing with the sort of analog input data that comes from an acceleromter to prevent sudden jumps in the readings (e.g. you knocked it) from having an undue impact on the processing. An MA is a convenient and easy way to do it. We simply input The current reading at index Ai and then increment Ai until it exceeds AL, then wrap it back around. You'll see this in the code later. I use numpy here because they execute very quickly (read: effeciently) and there are handy functions to make things simpler. Like .ones() to initialze all of AZa to a value of one — there's always by default 1G of gravity downwards.

After dealing with the accelerometer directly are declarations for those variables dealing with gravity. GX, etc., store the best (most recent) guess of what direction gravity is in, as once we start moving we have a combined acceleration of gravity plus the user's movement. We need this to subtract gravity back out so we know how the user is moving. Ideally this would be done with a gyroscope, but we don't have one of those so we make do.

# store gravity when fast is detected..
GX = 0
GY = 0
GZ = 1

# polar gravity
PGR = 0
PGA = -math.pi/2
PGB = 0

# screen gravity
PSGR = 1
PSGA = -math.pi/2
PSGB = 0

# accelerometer values
AX = 0
AY = 0
AZ = 0

# rotated for screen accelerometer values
GAX = 0
GAY = 0
GAZ = 0

PSGR are the polar coordinates of gravity in the screen, which is an accleration field that's always downwards. If you consider that the Model A might not be parallel to the screen while being waved about (e.g. it's held rotated) then we need to rotate the acceleration field it experiences back to screen normal. I'm actually not entirely sure about this — this was all new to me when I was writing it, so this is just a guess really. It seems to work though so I've left it in. In my experience most projects like this have fiddly bits like this.

AX etc. store the result of the moving average of the acceleromter data. GAX etc. store the current acceleration as from AX but rotated correctly for the screen.

last_G = 0

# timing information
last_time = time.time();

Imagine you're in a car traveling down the motorway at 100 kph. In one hour you will have travelled 100 km. Easy? That's simple integration, going from velocity to displacement. Acceleration though, is the rate of change in velocity, e.g. the speed at which the needle of the speedometer in the car climbs. So now imagine accelerating at 1 kph per second, after 10 seconds you'll be going 10 kph faster, so instead of 100 kph you're now going 110 kph. Apply that to the distance you've travelled and you have twice integration. (Fun fact: if you kept up that acceleration, after an hour you'd be going 3,700 kph and would have traveled 36,370 km. Or almost around the Earth.)

# brush info
BX = 0 # position
BY = 0
VX = 0 # velocity
VY = 0
P = 0 # amount of paint on brush
S = 0 # distance brush has traveled
last_stroke = 0

# seed random number generator
random.seed(time.time())

2.2.2. Functions

# =========
# functions
# =========

def polar(X, Y, Z):
    x = numpy.linalg.norm([X, Y, Z])
    if (x > 0):
        y = -math.atan2(Z, X)
        z = math.asin(Y / x)
    else:
        y = 0
        z = 0
    return (x, y, z)

def cartesian(X, A, B):
    x = 0 # don't bother - isn't used
    y = X * math.sin(B) * math.sin(A)
    z = X * math.cos(B)
    return (x, y, z)

def savereset():
    filename = SAVEDIR + os.sep + ("%i.png" % time.time())
    pygame.image.save(screen, filename)
    screen.fill((255, 255, 255))

In this scenario I've found a Unix timestamp to be the easiest way of doing this. It's simply the number of seconds since Jan. 1, 1970, but it's always going up and unless someone invents time travel won't repeat. You may have realized though that as the Pi doesn't have a real time clock, it may indeed count the same time over and over. A weakness that will have to be accepted. Besides, what are the odds someone would reset the screen at exactly the same number of seconds since the Pi was turned on twice? (A proper way to fix this though would be to check for an existing file first.)

2.2.3. Main program

# ============
# main program
# ============

fast = 0
notfast = 0
running = 1
while running:

running is what it sounds like and is used to keep the program continually looping in a while loop. When we want to quit we set running to 0, the loop finishes and then the program exits.

The main program loop consists of three phases. Phase 1 consists of basic tasks that need to be done over and over. Phase 2 consists of reading the accelerometer data and pre-processing it. Phase 3 consists of manipulating the paintbrush and canvas.

2.2.3.1. Phase 1

    # move time forward
    dt = time.time() - last_time
    last_time = time.time()

    # no changes made to the screen so far
    draw = 0

The next two bits of code deal with input. The first is keyboard input handled though PyGame. The second is GPIO input from the push button we installed, which we handle manually.

    # check for keyboard input
    event = pygame.event.poll()
    if event.type == pygame.QUIT:
        running = 0
    elif event.type == pygame.KEYDOWN:
        if event.key == pygame.K_q:
            running = 0
        elif event.key == pygame.K_r:
            savereset()
            draw = 1

pygame.KEYDOWN is a regular keypress. Once we know it's a keypress, we can check which key has been pressed. If it's the Q key we indicate we want to quit but setting running to 0. If it's the R key we save the screen, reset it, and then set draw to 1 so that we know to .flip() later.

    # check for GPIO input, but because it's a
    # pull down (goes from 1 to 0 when pressed)
    # flip logic
    button_now = not(GPIO.input(17))
    if button_now == 1 and button == 0:
        # the button was pressed
        savereset()
        draw = 1
    button = button_now    

The other thing we have to consider is what happens when the button is pressed and held down. In this case we only want to trigger a save and reset once, not multiple times. That's why we check not only if the buttonnow is 1, but also that button is 0, i.e. in the previous loop it wasn't pressed. We then set button to buttonnow so that when we hit the next loop we know it was pressed and don't reset the screen.

2.2.3.2. Phase 2

    # ===================
    # networking & sensor
    # ===================

    result = select.select([sock], [], [], 0)
    if len(result[0]) > 0:

        # read in data
        data = result[0][0].recvfrom(1024)
        a = data[0].split(",")
        AXa[Ai] = float(a[0])
        AYa[Ai] = float(a[1])
        AZa[Ai] = float(a[2])
        Ai = Ai + 1
        if Ai == AL:
            Ai = 0

        # moving averages for acceleration
        AX = numpy.sum(AXa) / AL
        AY = numpy.sum(AYa) / AL
        AZ = numpy.sum(AZa) / AL

        # combined acceleration for
        # working out resting gravity
        A = math.fabs(numpy.linalg.norm([AX,
                AY, AZ]) - 1)

        # in a slow moment store most recent 
        # direction of the gravitational field
        if A < 0.02 and (last_time - last_G) > 0.12:
            GX = AX
            GY = AY
            GZ = AZ
            (PGR, PGA, PGB) = polar(GX, GY, GZ)
            last_G = last_time

        # rotate to screen coordinates
        # and subtract gravity
        (PAR, PAA, PAB) = polar(AX, AY, AZ)
        (GAX, GAY, GAZ) = cartesian(PAR,
                PAA - PGA + PSGA, PAB - PGB + PSGB)
        GAZ = GAZ - PGR

So then once it's been established that it's OK to take an estimate, we do that by storing AX, etc., in GX, etc.. We then turn the estimate into polar coordinates and make a note when we made this estimate. After we take that estimate we proceed on normally and then rotate acceleration for the screen according to where gravity is. I'm sorry the maths here is complex and to be honest I don't really understand it. As near as I can tell it does work though, or at least does what we want it to. Basically the cartesian line takes the polar gravity and rotates it by how we know gravity to be rotated and then adds back on gravity as experienced by the monitor. The GAZ line after than subtracts gravity from its absolute direction. And that's it for Phase 2.

2.2.3.3. Phase 3

    # ==================
    # paintbrush physics
    # ==================

    # acceleration detection for paint strokes
    A = numpy.linalg.norm([GAY, GAZ])

    # detect moving quickly
    if A > 0.4 and fast != 1 and \
                last_time - last_stroke > 0.5:
        fast = 1
        notfast = 0
        scale = random.random() * 0.5 + 0.5
        BX = YRES * GAY * scale + XRES / 2 + \
                random.randint(-XRES/4, XRES/4)
        BY = YRES * GAZ * scale + YRES / 2 + \
                random.randint(-YRES/7, YRES/7)
        VX = 0
        VY = 0
        P = 100
        COLR = random.randint(0, 255)
        COLG = random.randint(0, 255)
        COLB = random.randint(0, 255)

There is only a low level of precision we can have over our control of where the virtual paintbrush is on screen given the level of and quality of input data that we have. To keep things interesting we use some random elements. We make an assumption that the user has probably aimed somewhere at the canvas and milk that for all it's worth. Where did the start the stroke though? The top of the canvas or the bottom? Left or right? We make a guess based on the direction of the accleration vector. How far to that direction though? We don't know so we randomly scale it. BX and BY is where we store the brush position. Both use YRES as a multiplier when going from acceleration vector to starting coordinate though as reality is square while our screen is rectangular. If we used XRES we'd end up disproportionately scaling the X position to the side, which would feel funny to the user.

We then reset the brush's velocity, VX and VY and the ammount of paint on the brush, P. We also then set the paint color randomly. I wish there was a nicer way to control this, but nothing simple springs to mind. We could have a tri-color LED randomly changing color and the paint color matches the LED color when the stroke starts. A project for someone perhaps. Either that or some variable resistors with some analog to digital interface so you could dial in a paint color. Awesome sounding, but actually a lot of work to do. One thing at a time eh?

    # detect stopping
    if fast == 1 and (A < 0.1 or ((BX > (XRES + 200) \
                or BX < -200) and (BY > (YRES + 200) \
                or BY < -200)) or P <= 0):
        notfast = notfast + dt
        if notfast >= 0.12:
            fast = 0
            BX = 0
            BY = 0
            last_stroke = last_time

    if fast == 1:
        # accelerate the paint brush
        VX = VX - GAY * dt * 170
        VY = VY - GAZ * dt * 170
        BX = BX + VX * dt * 120
        BY = BY + VY * dt * 120

The next integration is incrementing the brush position by adding on the current velocity. Which also must be factored by the timestep. And then another scaling factor, this time of 120. Realistically these factors should probably be adjusted for screen resolution but I haven't worked out a formula for that. These numbers work reasonably well with the resolutions I've tried though, so I've left them alone.

        # add splotches.... high velocity big 
        # splotches far apart, low small close
        if P > 0:
            V = numpy.linalg.norm([VX, VY])
            S = S + V
            d = A * random.randint(3, 5) * 25 + V

The first thing is to remember that this bit of code follows on from the last if statement, so is only run while the paintbrush is moving. And then it's only run if there's actually paint left on the brush. Vaguely I expect that the further the brush has been swung the more paint I expect to come off and the faster it's going the more paint to come off. V is calculated as the total velocity, and S is a running displacement. d is calculated as a rough estimtate of paint droplet spacing.

Let's look at d in a bit more detail. Paint droplets (probably) fly off due to two factors:

• Fluid mechanics. Roughly, I'm speaking of the affect of what happens when you move a glass of water too quickly.
• Air resistance. The force you feel acting on your hand when you stick it out the car window on a drive on a nice summer's day.

Both of these are rather complex subjects and therefore I've sort of lumped the two of them together as the produce similar results—paint flying off the brush. d is made up of A (our acceleration) times a random factor which is the fluid dynamics bit, and V is added for the air resistance bit. The random factor makes things a bit more interesting, perhaps taking into account things like globs of paint or hairs in the brush getting tangled. We also can't forget the random scaling factor of 25 which was added so that things are proportioned nicely on the screen. (This applies to the acceleration term only as velocity was already scaled in the previous code block.)

            if S > d:
                S = S - d
                P = P - pow(A*4, 2) * math.pi
                pygame.draw.circle(screen, (COLR, COLG, 
                        COLB), (int(BX), int(BY)), int(A*45))
                draw = 1

draw.circle() is the Pygame function for drawing a circle, which we're going to assume our paint droplets are. (More realistically they should probably be tear shaped.) We're drawing on the screen, in our random color at the paintbrush position (BX, BY). In this case int() isn't converting from a string, but from a floating point number to a whole integer—pixels on the screen at at specific coordinates. (It's the difference between 8.128 and 8.0. We need the latter as there's only pixel 8 and pixel 9, and no pixel in between.) A*45 is the paint droplet radius, and yes, 45 is another made up factor. We set draw to 1 so that we know to refresh the screen.

We're almost done.

    # push updates to the screen
    if draw == 1:
        pygame.display.flip()

2.2.4. Quitting

This actually surprisingly easy. If you remember from before about the while loop and running. And then about checking for the KEYDOWN of k_Q, that's half the quitting code right there. The other half is just tidying up. The first bit will get us out of the otherwise infinite loop.

# quit properly
GPIO.cleanup()
pygame.quit()

3. System Setup & Running

At least, done with the code. There are other nigly details to get things going. Most of that are regular issues with installing software or setting up the resolution to the monitor. Then there's the big one, networking.

3.1. Installing

What we've seen so far are two Python scripts. You can download them off of GitHub, copy to your SD card, and run almost immediately. The Model A though will need to have the XLoBorg library for Python installed.

This is a work in progress! Alternatively, we've also prepared a .deb package which can be used to install PiBrush on your Pi. These are availale on our PPA, for which we have directions. After setting up the PPA the package, installation is easy:

apt-get install pibrush

You then will need to edit /etc/default/pibrushd to match the specifics of your setup. That's it! There's a manpage if you need more help. It includes directions for setup on the Model A (client).

man pibrush

3.2. Networking

There are two ways to handle networking. The standard way would be to use a regular Wi-Fi access point (or router), with the Model B connected over either with a Wi-Fi dongle or an ethernet wire, and the Model A connected with a USB Wi-Fi dongle. The Wi-Fi access point then relays the information between the Model A and Model B. This is the setup in most homes and doesns't require anything special — see our wifi instructions here.

Then there's what we did for our display at the Ideas Bazaar, which is cut out the middle man. We used ad hoc Wi-Fi which doesns't rely on an existing network (but does require two Wi-Fi dongles). With ad hoc networking, the Pis communicate with each other directly. This means that the Pis aren't affected by a lack of Wi-Fi network, which is often the case when you're on the move. Let's look at how to do this.

First you'll need to tell the Pi that you want it to use ad hoc networking. You can do this by editing /etc/wpa_supplicant/wpa_supplicant.conf and adding the following lines:

network={
        ssid="pibrush"
        key_mgmt=NONE
        frequency=2432
        mode=1
}

This tells the Pi to search for the ad hoc network. Now, because there's no access point there's also no DHCP, which is the bit of software running on the access point responsible for telling computers how to talk to each other. Without that we have to tell the two Pis how to find each other manually. This means static IP addresses. We set these up in Debian by editing the /etc/network/interfaces file and removing the dhcp line and replacing it with this:

iface default inet static
address 192.168.31.1
netmask 255.255.255.0

On the Model A change the 31.1 to 31.2. The other file to edit is the /etc/hosts file, adding the following two lines:

192.168.31.1 modelb
192.168.31.2 modela

On the next boot the two Pis will talk to each other directly! You're all set to go! Good luck!

You can see complete configuration files online on GitHub here.

Warning! If you're relying on Wi-Fi to access your RaspberryPis, these changes WILL BREAK THAT! If you do this accidentally and get locked out you can always pop the SD card into another Linux PC and edit these configuration files back. Also, AN ETHERNET CABLE WILL STILL WORK! You should also be able to see the Wi-Fi network with your laptop, if you connect you can assign your laptop another IP like 192.168.31.3 and then your laptop and Pis should be able to talk.

4. Art

Here's what we made together at the Ideas Bazaar...